Da Vinci, Langley and their codes :
I finished reading Dan Brown's Da Vinci Code last week. It was a indeed a good read. The plot was laid down beautifully and events flowed smoothly. Although it had hitherto unheard (or atleast "not so popular") anecdotes from the life of Jesus, what amused me more were the numerous references to ciphers and codes and the facts surrounding them.
There was a page or two devoted to explaining the significance of PHI or the "Divine Proportion". It is also called the Golden ratio, the Golden Mean or Golden section. It is equal to 1.618 ( or more accurately 1.6180339887498948482.......) . I tried to read more about this interesting number and here is what i have been able to compile from various sources,
1. The number PHI can be represented as a nested radical in the form sqrt(1+sqrt(1+sqrt(1+......)))
2. It can be represented as a continuous fraction in the form 1+ 1/ (1+ 1/ (1 + 1/(........))).
3. Trigonometric formulas for PHI include 2* cos ( Pi/5) , 1/2 sec ( (2*Pi)/5) , 1/2 cosec (Pi/10).
4.Given a rectangle having sides in the ratio 1:PHI, partitioning the original rectangle into a square and new rectangle results in the new rectangle having sides with the ratio 1:PHI ( Iam still playing with this, although it is clear that if the length : breadth ratio is set to (sqrt(5)+1)/2, the rectangle would be Golden.
5.Successive points dividing a golden rectangle into squares lie on a logarithmic spiral.
6.The quotients of the adjacent terms in a Fibonacci series approach PHI.
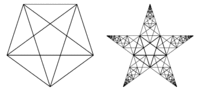
7. If a series of embedded pentagrams ( the five point star) is constructed to form a larger Pentagram and if the central Pentagram has centre at (0,0) and circum radius 1, then the subsequent pentagrams will have radii r(n) = 1/ PHI ^n.
The picture at the top illustrates the construction of the larger pentagram.
8. For a decagon ( 10 sided polygon ) the circumradius R= PHI * (length of the side of the decagon.)
9.A golden triangle is an isosceles triangle whose ratio of the hypotenuse to base is equal to PHI. In this case the vertex angle of the triangle would be 36 degrees.
10. 1/ PHI is equal to 1 - PHI.
11. From a golden triangle can be constructed a golden gnomon which is an obtuse isosceles triangle whose side to base ratio is 1/PHI.
12.Golden triangles and gnomons can be dissected into smaller triangles that are golden gnomons and golden triangles.
13. A Golden angle is the angle that divides a Full angle in the golden ratio. Considering the full angle 360 degrees, the golden angle is 360/(1+ PHI) which is equal to 137.5 degrees. Points separated by 137.5 degrees on a tightly bound spiral tend to form interlocking spirals winding in opposite directions and the number of spirals in these two families tend to be consecutive fibonacci numbers.
14. The arrangement of leaves in some plants ( called PHYLLOTAXIS) obey a number of subtle mathematical relationships. The florets in the head of a sunflower form two oppositely directed spirals, 55 of them clockwise and 34 counter clockwise (these are adjacent Fibonacci numbers :-)) ).
15.A similar phenomenon occurs for daisies, pineapples, pinecones, cauliflowers..etc.
This ubiquity of the divine proportion in nature points to an underlying sense of order in the chaos that surround us. What does this convey about the creator's intention? Well, it is for everyone to ponder!
And now about the folks at Langley.....what do you have to say about Kryptos ?





Dear, You already found your true 'North' to start your sailing.. you got plenty of time left out in your life to complete all your wishlist. I am sure everything will be 'hunky- dory' at the end.
ReplyDeleteRemember, to do tick mark the ones as you do it.
I'm writing a research paper on the Golden Ratio for my senior seminar class. I came across your blog while doing my research, and can see that you have put a great deal of thought into what you have read. If you're still continuing your interest in this amazing number, please let me know, it would be great to talk about my research with another math enthousiast!
ReplyDeleteHey tink,,
ReplyDeleteIt has been a while since i wrote this piece. I had investigated the properties of this number as it struck me as an amazing ratio. If you are a maths enthusiast, you may find some good material here http://mathworld.wolfram.com